Brian (Po-Yen) Tung
Materials on a Data Diet: Searching for the Best with AI and Minimal Input

I’m a Machine Learning Scientist at MatNex, where I collaborate with a brilliant team of scientists to develop AI-driven methods that accelerate materials discovery — all with the goal of enabling a net-zero future. I drive the development of our discovery pipeline, focusing on active learning and reinforcement learning strategies for efficient exploration.
Before this, I was a Postdoc at Cambridge from 2021 to 2024. I had the pleasure of being affiliated with Peterhouse, the university’s oldest college — a place steeped in history and charm. I got my PhD in Materials Science at Max Planck Instuitute under the supervision of Prof. Dirk Raabe.
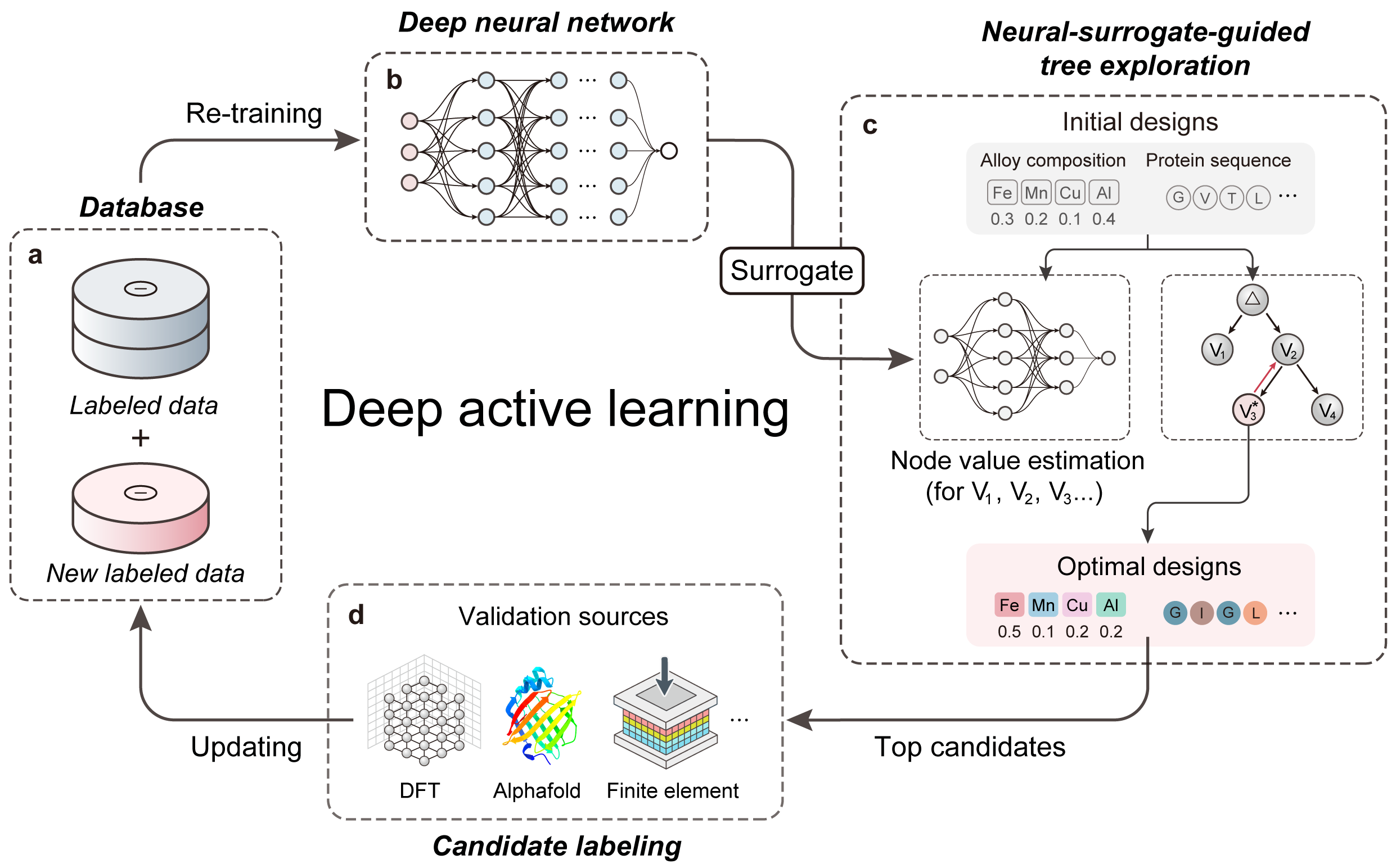
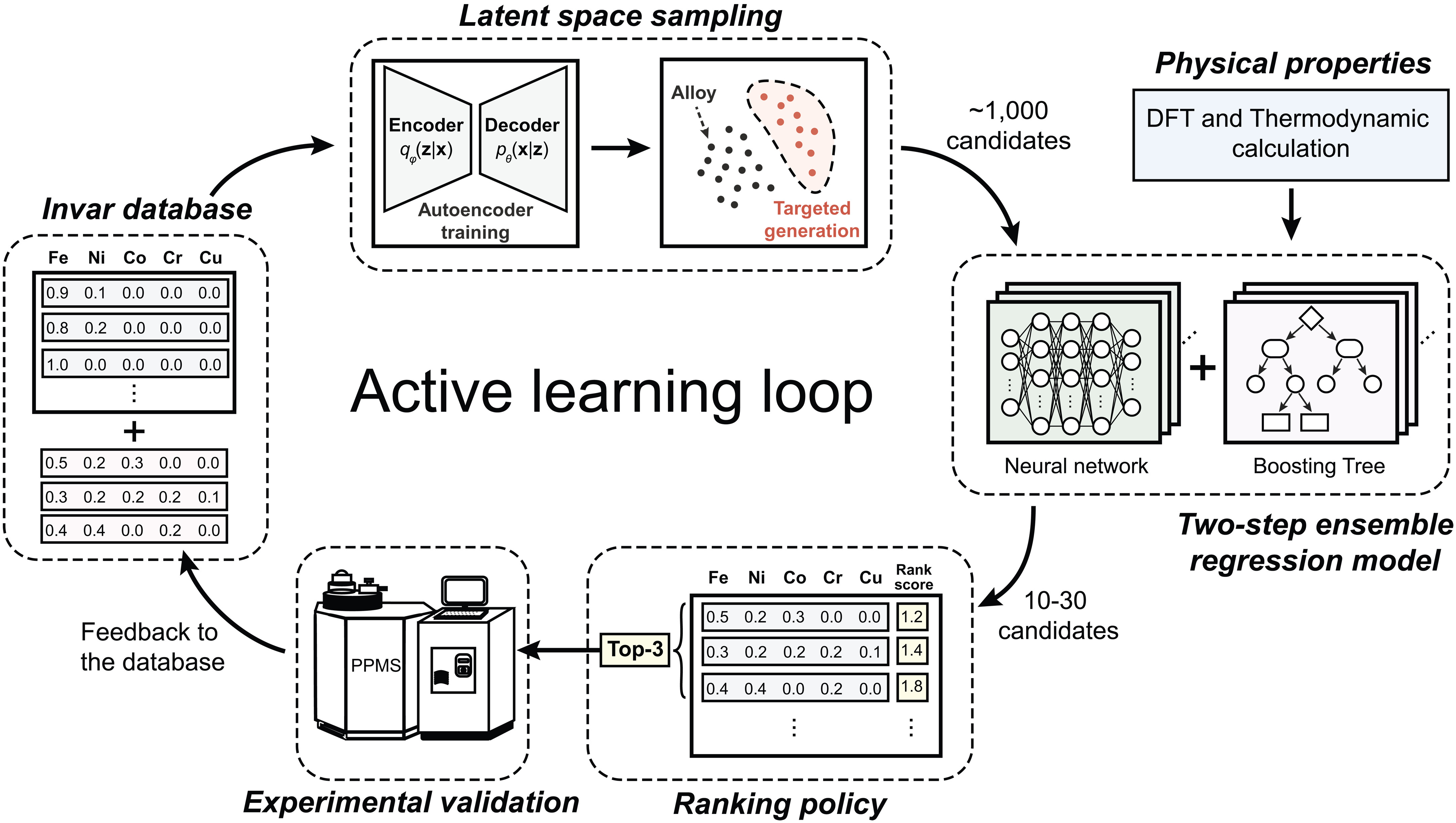
Some of my most notable work before joining MatNex includes the development of DANTE, a general search framework designed to navigate high-dimensional spaces with minimal data. I also co-led the creation of active learning pipelines for high-entropy alloys in 2022, which contributed to a rapid discovery of 2 Invar alloys in just 3 months — published in Science.
Latest posts
Selected publications
- Next Materials
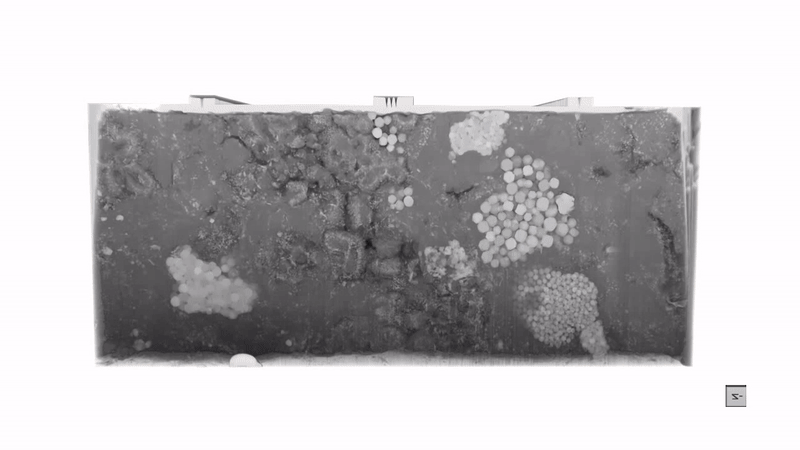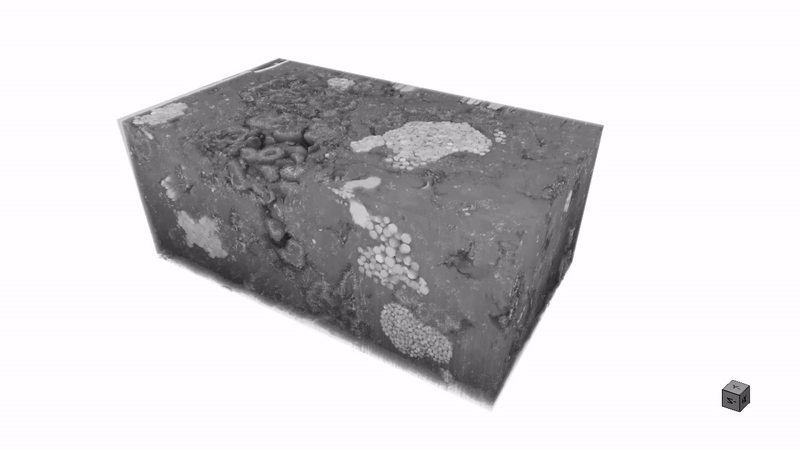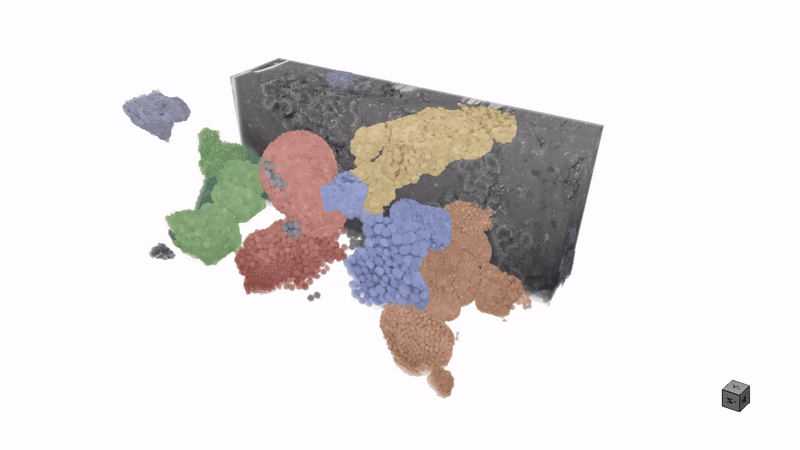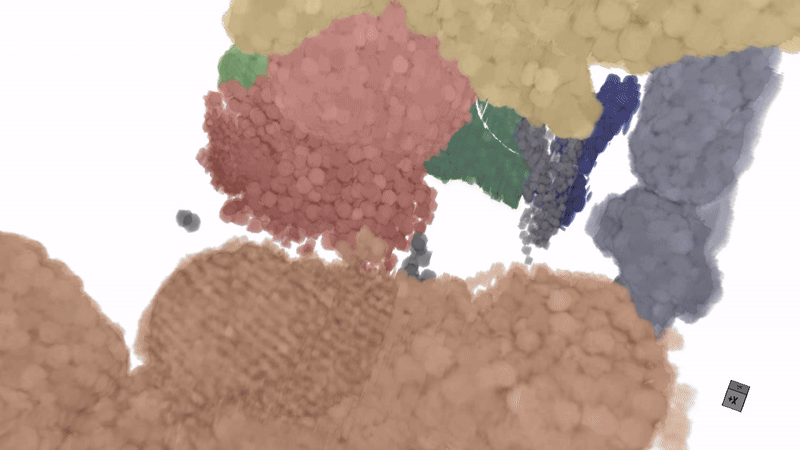 Efficient microstructure segmentation in three-dimensional imaging: Combining few-shot learning with the segment anything modelNext Materials, 2025
Efficient microstructure segmentation in three-dimensional imaging: Combining few-shot learning with the segment anything modelNext Materials, 2025